原文地址:http://mp.weixin.qq.com/s/Wj2MOPGvJJIkRrz1bsqbCw
作者:数据取经团-王嘉琪
在机器学习和数据挖掘常用的方法中,常规的建模思路是输入给定的训练数据集(类别标签已知),通过一系列的训练建立预测模型,通过将需要预测的数据输入到训练完成的模型中得到预测结果。然而,并非所有的方法都包含了训练过程,K近邻算法就是其中之一。
K近邻的基本思想
K近邻算法(KNN)是一种常用的基本分类(亦可运用于回归)方法。其基本思想是,输入一个给定的训练数据集,包含了X和标签Y。对于新的数据,在预测分类时,根据指定的参数K,对于每个需要预测的个体,找出距离该点最近的K个训练集的样本点,通过这些样本点的所属类别,以投票表决的方式来进行类别预测。可以看出,在输入训练数据集到预测的过程中,该算法并没有显著的模型训练过程。
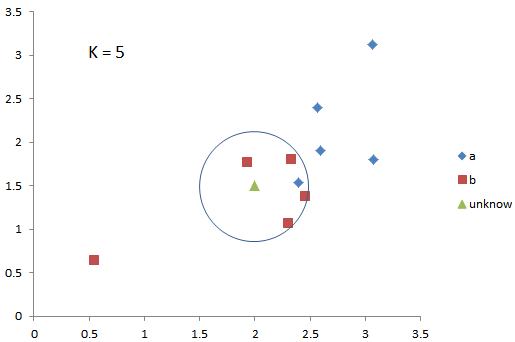
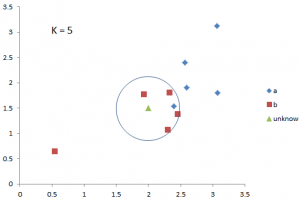
例如下图,二维空间中,已知10个训练集的样本点,分属于AB两个类别,对于需要预测的样本点,在K=5时,找到距离其最近的5个样本点,其中4个点属于B类,则根据规则,该点的预测类别也为B类
常规的K近邻算法流程:
输入:训练数据集T{(x1,y1),(x2,y2)…(xN,yN)},参数K,需要预测的数据集实例x
输出:实例x的类别y
① 根据给定的距离度量,在训练集T中找出K个距离x最近的样本点集合记作Nk(x);
② 在Nk(x)中根据分类规则(一般为投票表决)决定x的类别y
作为较为简单的分类算法,K近邻算法有着一定的优势:首先,K近邻算法不需要训练过程,相比于较为复杂的模型,降低了训练模型的时间成本,具有较高的效率;其次,K近邻算法概念简单,容易实现,可解释性强。在实际应用中,K近邻方法可以作为一种在线技术,只需要不断添加新的训练数据,而不需要重复训练模型。
相对地,这种方法的缺陷也是显而易见的。第一,当样本类别分布非常不均衡的时候,预测偏差会增大(分类往往重视多数类而忽视少数类);第二,KNN的算法在对每一个个体的预测都是一次全局计算,且当数据量特别大的时候,计算量非常大,从而影响效率;第三,KNN的思想决定了其预测工作必须依赖存储的训练数据集,需要较高的存储成本。
K近邻算法的注意点
距离的度量
在KNN预测过程中,距离的计算十分重要,计算点Xi和点Xj的距离,通常可以采用明氏距离:
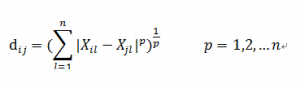
当p=1时,为曼哈顿距离,曼哈顿距离就是点之间绝对轴距之和,但是在n维空间中,曼哈顿距离并不是点与点之间的最短距离。所以通常采用的是欧氏距离(p=2)来测量两点之间的距离:
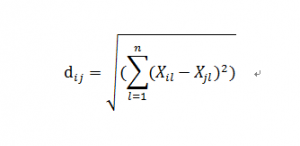
在二维或三维空间中,欧氏距离就是两点之间的实际直线距离(最短距离),目前欧氏距离在相关的算法中最为常用。但实际上有时欧氏距离(或者明氏距离)也有显著的缺陷,它将样本的不同属性(即各指标或各变量)之间的差别等同看待,但实际中往往并非如此。当n维变量之间存在联系时,亦可以采用马氏距离来衡量点之间的距离(相似度):
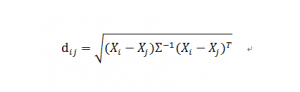
数据的量纲问题
在计算点与点的距离的时候,有时变量间量纲的存在会影响距离的大小,这就不可避免地导致数量及较大的变量有时能够“决定”距离,而数量级小的变量的差异则会被“忽略”。因此多数情况下,需要对数据进行处理以避免这种影响。
常见的处理方法有归一化和标准化。归一化方法是将变量的大小映射到0-1之间,公式如下:
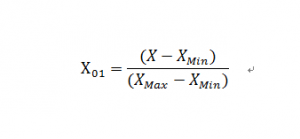
标准化则是变量减去均值再除以标准差,在统计学上经常会使用,公式如下:
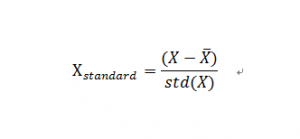
这两种方法有效的将变量之间绝对数的量纲差异消除,即将所有的X变量“等同对待”,某种程度上“放大”了变量的相对差异,因此并非适用于所有情况。
K的确定
K值的选择也会对K近邻算法的结果产生较大影响。当K值较小时,学习的“近似误差”会比较小,只有与目标点最为接近的几个样本点才会起作用,但会引起学习的“估计误差”增大,因为此时预测结果会对近邻点极为敏感,容易受噪声的影响;当K值较大时,可以减少学习的“估计误差”,但“近似误差”则会变得较大,因为一些距离目标点相对较远的样本点会产生影响,同时K的增大也意味着模型整体变得“简单”。
在应用中K通常会取一个较小的变量,并采用交叉验证法来选择最优的K。
效率问题
当数据量较小时,对最近邻点的寻找可以采用全局搜索的方法,但随着样本点数量的增加,对每个目标点进行这种搜索方法不再具备可行性,因此需要对搜索方法进行优化。目前已有的方法例如KD树等,从数据的排列、存储结构等方面进行优化,具体原理本文不作阐述,当前主流的机器学习平台(如shkearn等)已经实现了一定的效率优化。
K近邻算法的简单实现:
首先,加载本次实践的数据(马匹疝病的生存预测),构建加载函数:
import numpy as np
#数据集读取函数
def get_data(file_name,sep='\t'): data_open = open(file_name) lines = data_open.readlines() data = []
for line in lines: line = line.replace('\n','') line = line.split(sep) a=[]
for value in line: value = float(value) a.append(value) data.append(a)
return np.array(data)
分别加载训练数据集和测试数据集。
#训练集读取
horse_train = get_data(u'C:\\Users\\intern\\Desktop\\example\ \机器学习算法实现最终版\\horseColicTraining.txt') horse_train_x = horse_train[:,range(horse_train.shape[1]-1)] horse_train_y = horse_train[:,horse_train.shape[1]-1]
#测试集读取
horse_test = get_data(u'C:\\Users\\intern\\Desktop\\example\ \机器学习算法实现最终版\\horseColicTest.txt') horse_test_x = horse_test[:,range(horse_test.shape[1]-1)] horse_test_y = horse_test[:,horse_test.shape[1]-1]
接下来定义KNN模型,首先将定义类knn_model,实例化类的同时将训练数据集(X和Y类别)传入
def standard_zeromean(self,x): #0-1标准化函数
return(x - self.train_data_x.mean(axis=0))/self.train_data_x.std(axis=0)
def standard_01(self,x): #标准化函数
return(x - self.train_data_x.min(axis=0))/(self.train_data_x.max(axis=0)-self.train_data_x.min(axis=0))
分别定义归一化函数函数和标准化函数(用于对数据的预处理),函数包含在knn_model类中
def standard_zeromean(self,x): #0-1标准化函数 return(x - self.train_data_x.mean(axis=0))/self.train_data_x.std(axis=0)def standard_01(self,x): #标准化函数 return(x - self.train_data_x.min(axis=0))/(self.train_data_x.max(axis=0)-self.train_data_x.min(axis=0))
预测函数(单点):在对一个新的样本点的类别预测时,首先计算出该样本点x到训练集所有点的距离,然后找出距离最近的K个样本点,对这些样本点所属类别进行分类汇总,找出最多的类,作为预测结果。函数包含在knn_model类中
def predict_1line(self,x,k,train_x,train_y): #对一行数据的预测
distance = ((train_x-x)**2).sum(axis=1)
mink_dis = np.sort(distance)[:k]
def isin(a):
return(a in maxk_dis)
distance = distance.reshape(distance.shape[0],1)
sel_lab=np.apply_along_axis(isin,1,distance)
type_pre = np.unique(train_y[sel_lab])[0]
for i in range(1,len(np.unique(train_y[sel_lab]))):
if sum(train_y[sel_lab] == np.unique(train_y[sel_lab])[i]) > sum(train_y[sel_lab] == np.unique(train_y[sel_lab])[i-1]):
type_pre = np.unique(train_y[sel_lab])[i]
return(type_pre)
预测函数(多记录):当根据传入的参数std来决定对数据集是否进行标准化处理,对大量的预测数据记录进行预测(调用predict_1line函数)。函数包含在knn_model类中
def predict(self,x,k=10,std=None): #预测函数
type_pred = []
if std == "zeromean":
x = self.standard_zeromean(x)
for i in range(x.shape[0]):
type_pred.append(self.predict_1line(x[i,:],k,self.train_data_x_std,self.train_data_y))
elif std == "0-1":
x = self.standard_01(x)
for i in range(x.shape[0]):
type_pred.append(self.predict_1line(x[i,:],k,self.train_data_x_01,self.train_data_y))
else:
for i in range(x.shape[0]):
type_pred.append(self.predict_1line(x[i,:],k,self.train_data_x,self.train_data_y))
return(np.array(type_pred))
准确度评价函数:对预测函数调用,可以直接通过输入测试数据集X和正确类别Y来评估预测的准确度。函数包含在knn_model类中
def Accuracy(self,x,y,k=10,std=None): #预测准确度的评价y_pre = self.predict(x,k=k,std=std) Accuracy = sum(y_pre == y)/float(len(y))
return(Accuracy)
采用马匹疝病数据集进行测试,设置的K=5,第一次测试未进行标准化,第二次测试进行归一化处理
#采用之前的horse数据集进行测试
knn_horse = knn_model(horse_train_x,horse_train_y) #将训练数据集的自变量和目标变量输入模型
#设置近邻数为5,未标准化的预测结果
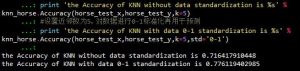
print 'the Accuracy of KNN without data standardization is %s' % knn_horse.Accuracy(horse_test_x,horse_test_y,k=5)
#设置近邻数为5,对数据进行0-1标准化再用于预测
print 'the Accuracy of KNN with data 0-1 standardization is %s' % knn_horse.Accuracy(horse_test_x,horse_test_y,k=5,std='0-1')
下图输出了测试的结果,可以看出,在经过了归一化处理之后,KNN的预测的准确度有了显著的提升(去量纲处理方式有时也不适用)
Sklearn模块训练示例
Python的sklearn模块包含了KNN模型,并且可以采用KD树等算法的提升效率,下面给出了用sklearn模块对数据集的归一化处理和KNN建模,在建模过程中搜索效果最佳的参数K并且进行预测,为了提升泛化能力,模型采用了5折交叉验证。
#sklearn模块knn选择最佳参数K建模示例
from sklearn.preprocessing import StandardScaler #模块:标准化函数(效果一般)
from sklearn.preprocessing import MinMaxScaler #模块:01标准化函数
from sklearn.neighbors import KNeighborsClassifier #模块:KNN分类模型
from sklearn.pipeline import Pipeline #管道串联模块
from sklearn.grid_search import GridSearchCV #网格搜索模块
#管道串联标准化步骤和建模步骤(暂时选用01标准化)
pipe_process = Pipeline([('scale_m',MinMaxScaler()),('knn_sklearn',KNeighborsClassifier())])
#传入KNN建模参数n_neighbors,候选值的范围包含了整数3-20
parameters = {'knn_sklearn__n_neighbors':np.array(range(3,21))}
#网格参数搜索,输入之前的模型流程pipe_process,候选参数parameters,并且设置5折交叉验证
gs = GridSearchCV(pipe_process,parameters,verbose=2,refit=True,cv=5) #设置备选参数组
gs.fit(horse_train_x,horse_train_y) #模型训练过程
print gs.best_params_,gs.best_score_ #查看最佳参数和评分(准确度)
#最佳参数的KNN建模对预测数据预测效果)
print 'The Accuracy of KNeighborsClassifier model with best parameter and MinMaxScaler is',gs.score(horse_test_x,horse_test_y)
经过对归一化的数据集KNN建模,从3-20对K值进行尝试,我们发现当K等于20的时候效果较好,对测试集的预测准确度可以超过80%