34 R非参数回归

34.1 模型

线性回归模型可以看成非线性回归模型的特例: \[Y = f(X) + \varepsilon\] 其中\(f(x)\)为未知的回归函数。

参数方法：假定\(f(x)\)具有某种形式，如

\(f(x) = a + b x\): 线性回归；
\(f(x) = a + b x + c x^2\):　二次多项式回归；
\(f(x) = A e^{bx}\): 指数模型，等等。

二次多项式回归可以令\(X_1 = x, X_2 = x^2\)，变成二元回归模型来解决。指数模型可以令\(z = \ln Y\), 模型化为\(z = a + bx\)。有一些曲线模型可以通过变换化为线性回归。

在多元情形，一般的非线性回归模型为 \[ Y = f(x_1, x_2, \dots, x_p) + \varepsilon \] 但是这样可选的模型就过于复杂，难以把握。比较简单的是不考虑变量之间交互作用的可加模型：

\[ Y = \sum_{j=1}^p f_j(x_j) + \varepsilon \] 其中\(f_j(\cdot)\)是未知的回归函数，需要满足一定的光滑性条件。

\(f_j(\cdot)\)可以是参数形式的，比如二次多项式、三次多项式、阶梯函数等。较好的一种选择是使用三次样条函数。

34.2 样条平滑

为了得到一般性的\(Y\)与\(X\)的曲线关系\(f(x)\)的估计，可以使用样条函数。三次样条函数将实数轴用若干个节点(knots) \(\{ z_k \}\)分成几段，每一段上\(\hat f(x)\)为三次多项式，函数在节点处有连续的二阶导数。样条函数是光滑的分段三次多项式。

用样条函数估计\(f(x)\)的准则是曲线接近各观测值点 \((x_i, y_i)\)，同时曲线足够光滑。

在R中用smooth.spline函数进行样条曲线拟合。取每个自变量\(x_i\)处为一个节点，对于给定的某个光滑度/模型复杂度系数值\(\lambda\)，求函数\(f(x)\)使得 \[ \min_{f(\cdot)} \left\{ \sum_i [y_i - f(x_i)]^2 + \lambda \int [f''(x)]^2 \,dx \right\} \] \(\lambda\)越大，所得的曲线越光滑。 smooth.spline()函数可以通过交叉验证方法自动取得一个对于预测最优的光滑参数\(\lambda\)值，也可以通过df=选项指定一个等效自由度，等效自由度越大，模型越复杂，曲线光滑程度越低。 df值相当于多元线性回归中的自变量个数。

如

set.seed(1)
nsamp <- 30
x <- runif(nsamp, -10, 10)
xx <- seq(-10, 10, length.out=100)
x <- sort(x)
y <- 10*sin(x/10*pi)^2 + rnorm(nsamp,0,0.3)
plot(x, y)
curve(10*sin(x/10*pi)^2, -10, 10, add=TRUE, lwd=2)

library(splines)
res <- smooth.spline(x, y)
lines(spline(x, res$y), col="red")
res2 <- loess(y ~ x, degree=2, span=0.3)
lines(xx, predict(res2, newdata=data.frame(x=xx)), 
      col="blue")
legend("top", lwd=c(2,1,1), 
       col=c("black", "red", "blue"),
       legend=c("真实函数关系", "样条平滑结果", "局部线性拟合"))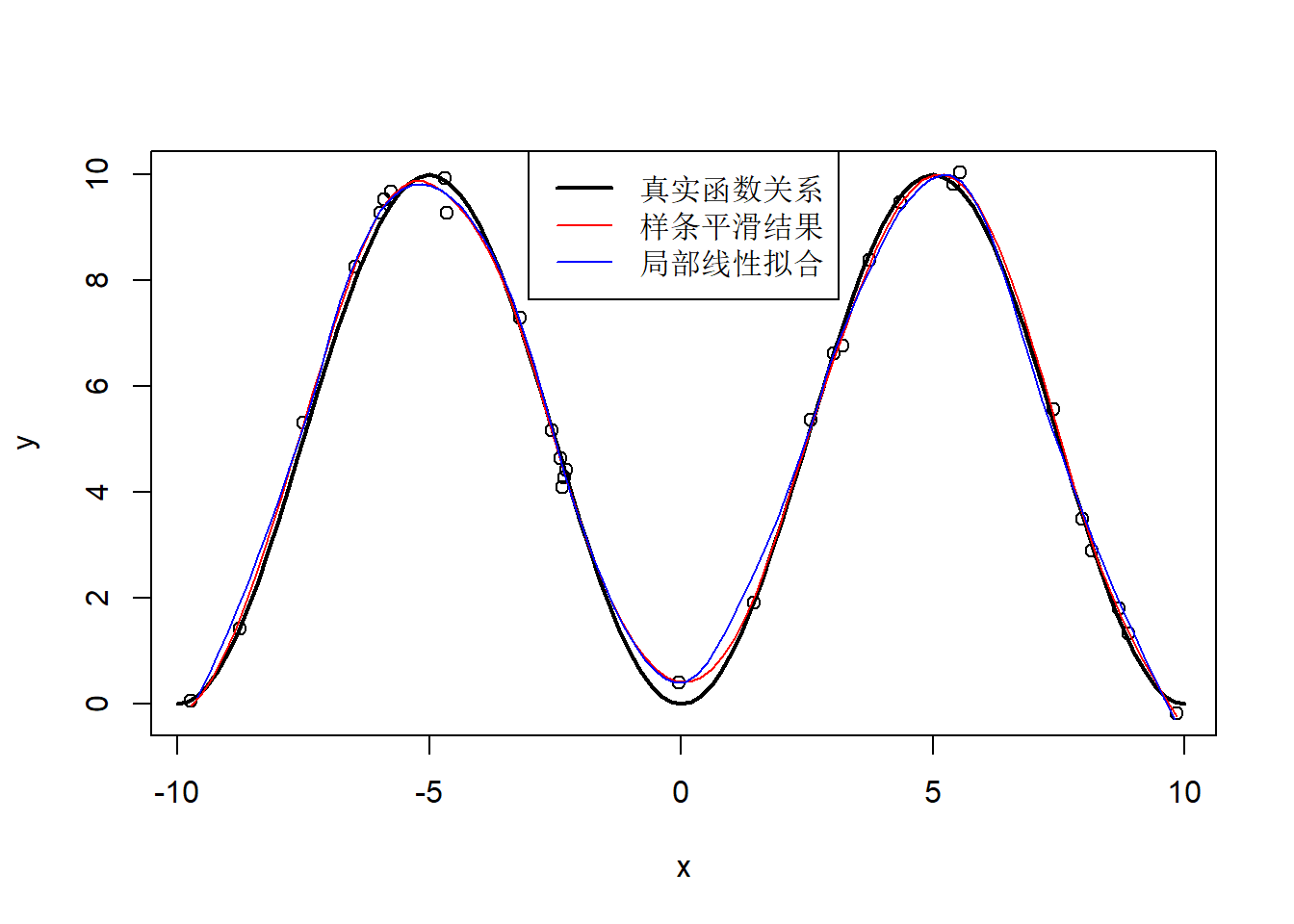

图34.1: 曲线平滑示例

其中res的元素y为拟合值，用spline(x,y)从一组散点输出光滑曲线以便用lines()函数绘图。

R函数splines(x,y)不是做样条平滑，而是做样条插值，其结果是在原始的自变量x范围内产生等间隔距离的格子点值，输出包含格子点上的样条插值x和y坐标的列表。样条平滑曲线不需要穿过输入的各个散点，但是插值则需要穿过输入的各个散点。

R函数approx(x,y)用线性插值方法产生线性插值后的连续函数在等间隔的横坐标上的坐标值。

34.3 局部多项式曲线平滑

另一种非参数的拟合非线性回归曲线\(f(x)\)的方法是对每个自变量\(x\) 处选一个局部的小邻域，用这个小邻域附近的\((x_i, y_i)\)点拟合一个局部的零次、一次或二次多项式，用拟合的局部多项式在\(x\)处的值作为回归函数在\(x\)处的值的估计。

局部零次多项式的方法叫做核回归，公式为 \[ \hat f(x) = \frac{\sum\limits_{i = 1}^n {K\left( {\frac{{x - X_i }}{h}} \right)Y_i } } {\sum\limits_{i = 1}^n {K\left( {\frac{{x - X_i }}{h}} \right)} } \] 其中\(K(\cdot)\)称为核函数，是类似标准正态密度这样的中间高两边低的可以用来加权的函数，比如，双三次核函数： \[ K(x) = \left\{ {\begin{array}{*{20}c} {\left( {1 - \left| x \right|^3 } \right)^3 } & {\left| x \right| \leq 1} \\ 0 & \mbox{其它} \\ \end{array}} \right. \]

kernel.dcube <- function(u){
  y <- numeric(length(u))
  sele <- (abs(u) < 1)
  y[sele] <- (1 - abs(u[sele])^3)^3
  y
}
curve(kernel.dcube, -1.5, 1.5, main="双三次核函数")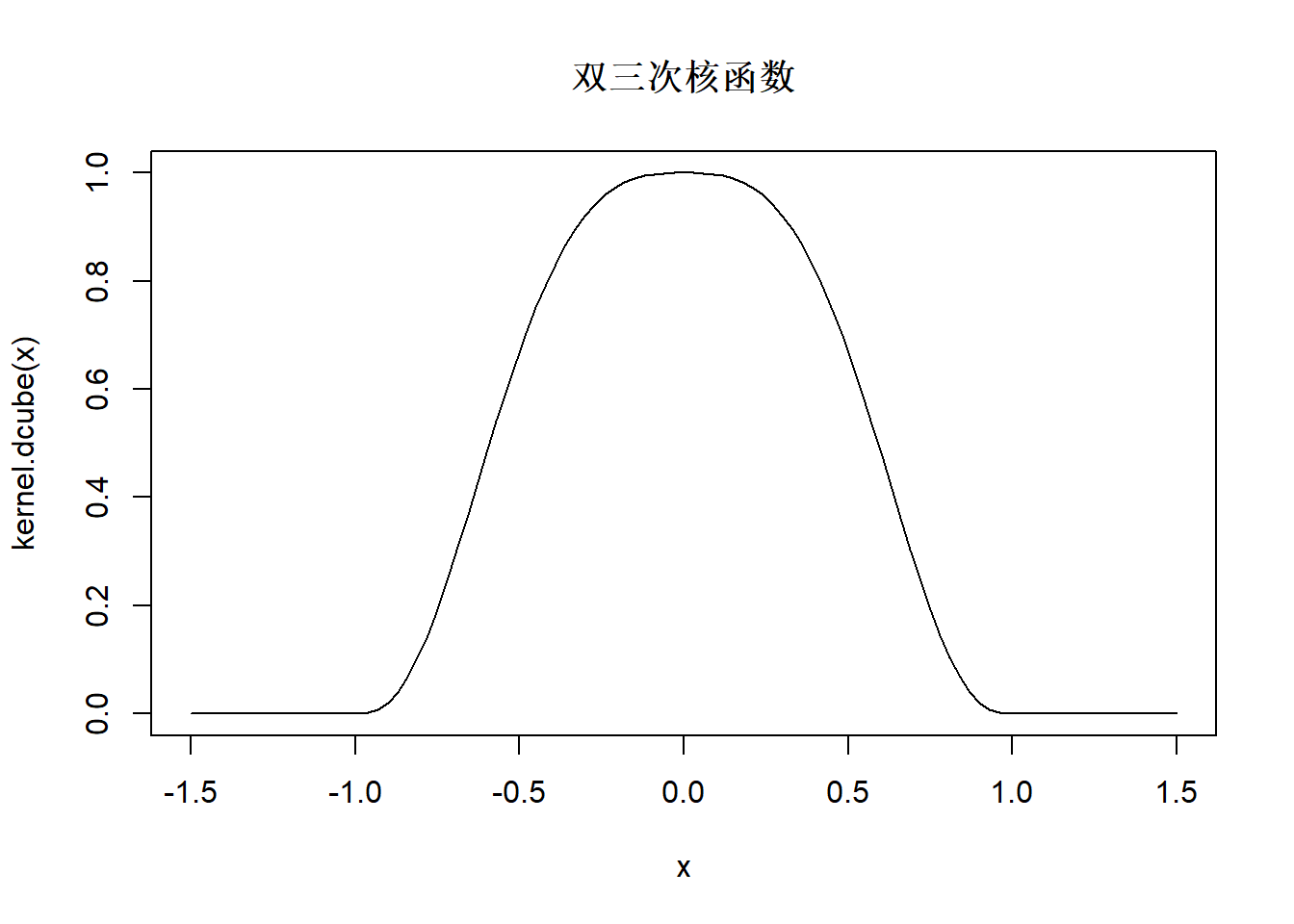

图34.2: 双三次核函数

参数\(h\)称为窗宽， \(h\)越大，参与平均的点越多，曲线越光滑，回归复杂度越低。 \(h\)选取可以用交叉验证方法。

R扩展包KernSmooth的函数 locpoly(x, y, degree=1, bandwidth=0.25)可以计算核回归，其中bandwidth是输入的窗宽，函数dpill(x,y)可以帮助确定窗宽。如 locpoly(x, y, degree=1, bandwidth=dpill(x,y))。 stats包的ksmooth()函数也可以计算核回归。

当局部拟合的是一次或者二次多项式时，这种曲线拟合方法叫做局部多项式回归。 R函数loess(y ~ x, degree=1, span=0.75)拟合局部线性函数，用span=控制结果的光滑度， span是局部拟合所用的点的比例，越接近于1结果越光滑。取degree=2拟合局部二次多项式函数。见图34.1。

34.4 样条函数变换

\(m\)个节点的三次样条函数需要\(m+4\)个参数。因为每段需要\(4\)个参数， \(m+1\)段需要\(4m+4\)个参数，而在\(m\)个节点上连续、一阶导数连续、二阶导数连续构成三个约束条件，所以参数个数为\(m+4\)个。

自然样条函数假定函数在最左边一段和最右边一段为线性函数，这样\(m\)个节点需要\(m+2\)个参数。 R的lm()函数中对自变量x指定ns(x) 可以对输入的x指定作自然样条变换， ns()可以用df=指定自由度作为曲线复杂度的度量。如

set.seed(1)
nsamp <- 30
x <- runif(nsamp, -10, 10)
xx <- seq(-10, 10, length.out=100)
x <- sort(x)
y <- 10*sin(x/10*pi)^2 + rnorm(nsamp,0,0.3)
plot(x, y)
curve(10*sin(x/10*pi)^2, -10, 10, add=TRUE, lwd=2)

res <- lm(y ~ ns(x, df=4))
lines(xx, predict(res, newdata=data.frame(x=xx)), 
      col="red")
res2 <- lm(y ~ ns(x, df=8))
lines(xx, predict(res2, newdata=data.frame(x=xx)), 
      col="blue")
legend("top", lwd=c(2,1,1), 
       col=c("black", "red", "blue"),
       legend=c("真实函数关系", "ns(df=4)", "ns(df=8)"))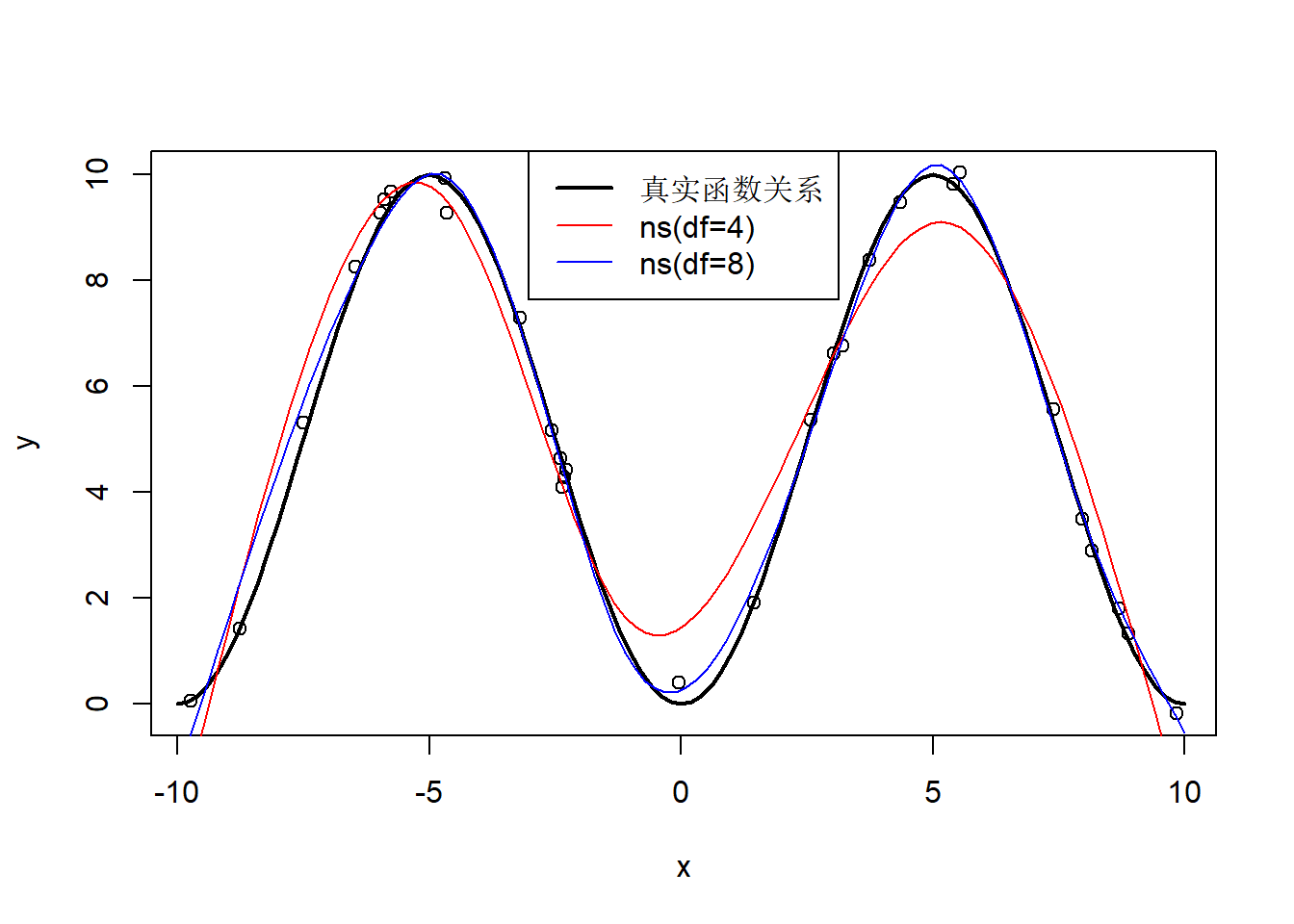

图34.3: 自然样条回归示例

在多元回归中也可以用ns(x)对单个自变量引入非线性。

34.5 线性可加模型

虽然在用lm()作多元回归时可以用ns()、poly()等函数引入非线性成分，但需要指定复杂度参数。对可加模型 \[ Y = \sum_{j=1}^p f_j(x_j) + \varepsilon \] 最好能从数据中自动确定\(f_j(\cdot)\)的复杂度（光滑度）参数。

R扩展包mgcv的gam()函数可以执行这样的可加模型的非参数回归拟合。模型中可以用s(x)指定x的样条平滑，用lo(x)指定x的局部多项式平滑。具体的计算是迭代地对每个自变量\(x_j\)进行，估计\(x_j\)的平滑函数\(f_j(\cdot)\)时，采用数据\(\tilde y = Y - \sum_{k \neq j} f_k(x_k)\)，迭代估计到结果基本不变为止。

例如，MASS包的rock数据框是石油勘探中12块岩石样本分别产生4个切片得到的测量数据，共48个观测，因变量是渗透率(permeability)，自变量为area, peri, shape。

先作线性回归：

lm.rock <- lm(log(perm) ~ area + peri + shape, data=rock)
summary(lm.rock)

## 
## Call:
## lm(formula = log(perm) ~ area + peri + shape, data = rock)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.8092 -0.5413  0.1734  0.6493  1.4788 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  5.333e+00  5.487e-01   9.720 1.59e-12 ***
## area         4.850e-04  8.657e-05   5.602 1.29e-06 ***
## peri        -1.527e-03  1.770e-04  -8.623 5.24e-11 ***
## shape        1.757e+00  1.756e+00   1.000    0.323    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.8521 on 44 degrees of freedom
## Multiple R-squared:  0.7483, Adjusted R-squared:  0.7311 
## F-statistic:  43.6 on 3 and 44 DF,  p-value: 3.094e-13

其中shape变量不显著。可能的原因有：

shape与因变量没有关系；
样本量不足；
shape与因变量之间有非线性关系，该非线性无法用线性近似。

用样条平滑的gam()建模：

library(mgcv)

## 载入需要的程辑包：nlme

## 
## 载入程辑包：'nlme'

## The following object is masked from 'package:dplyr':
## 
##     collapse

## This is mgcv 1.8-38. For overview type 'help("mgcv-package")'.

gam.rock1 <- gam(
  log(perm) ~ s(area) + s(peri) + s(shape), data=rock)
summary(gam.rock1)

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## log(perm) ~ s(area) + s(peri) + s(shape)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   5.1075     0.1222   41.81   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##            edf Ref.df     F  p-value    
## s(area)  1.000  1.000 29.13 3.07e-06 ***
## s(peri)  1.000  1.000 71.30  < 2e-16 ***
## s(shape) 1.402  1.705  0.58    0.437    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.735   Deviance explained = 75.4%
## GCV = 0.78865  Scale est. = 0.71631   n = 48

对gam()回归结果做单个变量的曲线拟合图：

plot(gam.rock1)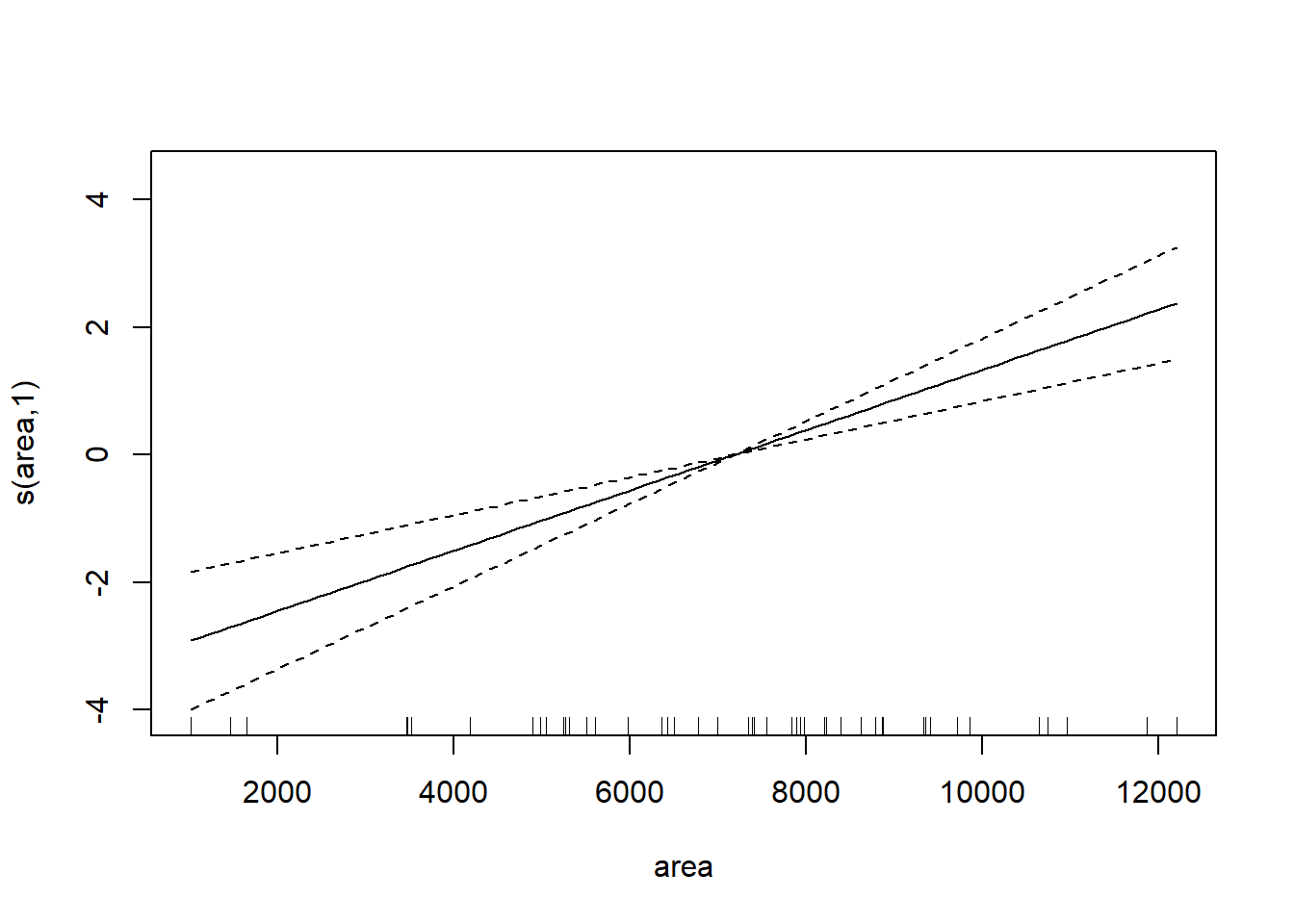

图34.4: 渗透率gam建模

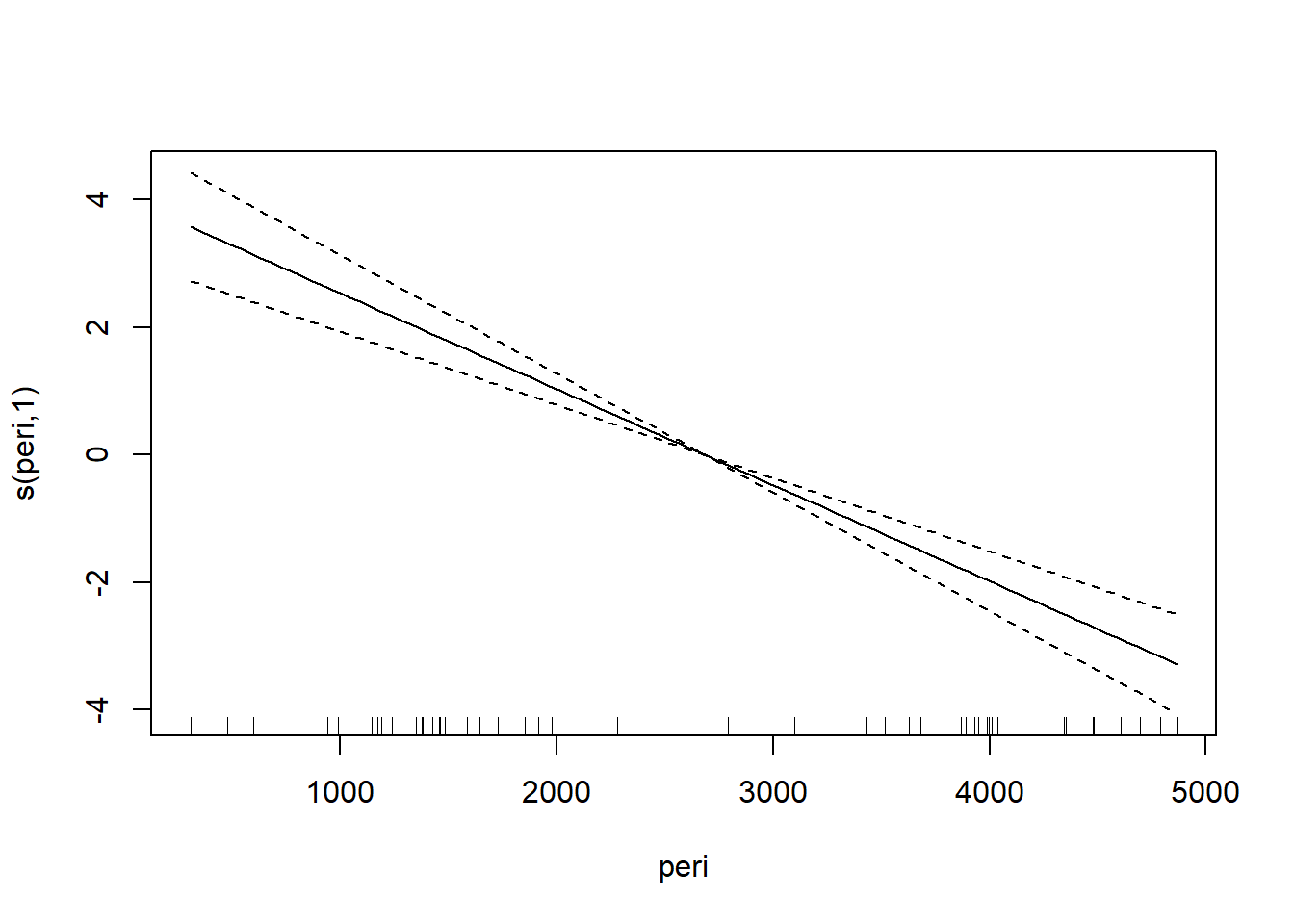
图34.5: 渗透率gam建模

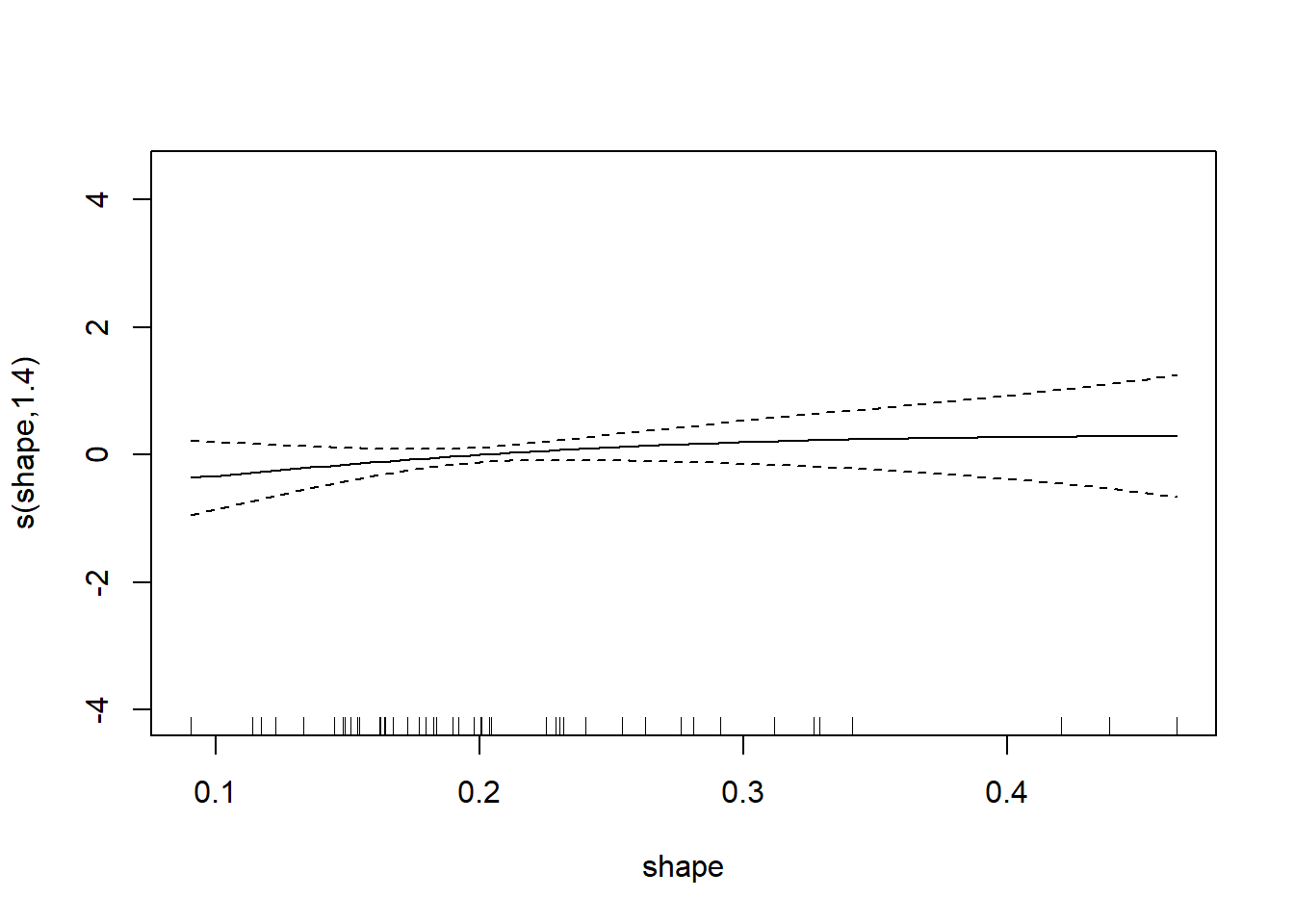
图34.6: 渗透率gam建模

可以看出三条曲线都基本不需要非线性。比较两个模型：

anova(lm.rock, gam.rock1)

## Analysis of Variance Table
## 
## Model 1: log(perm) ~ area + peri + shape
## Model 2: log(perm) ~ s(area) + s(peri) + s(shape)
##   Res.Df    RSS      Df Sum of Sq      F Pr(>F)
## 1 44.000 31.949                                
## 2 43.598 31.230 0.40237   0.71914 2.4951  0.125

结果也不显著，说明线性模型是可取的。