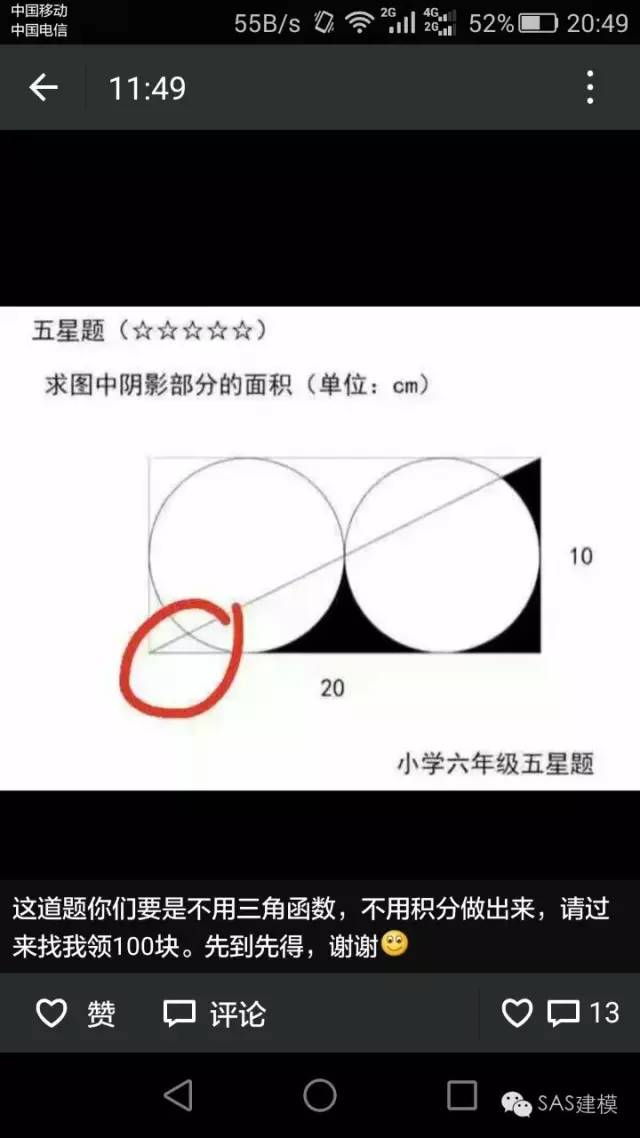
问题的起源来自万能的pyq:
Okay,看到有奖金,小编很开心,不用三角函数不用积分,那就用一下蒙特卡洛随机投点咯~
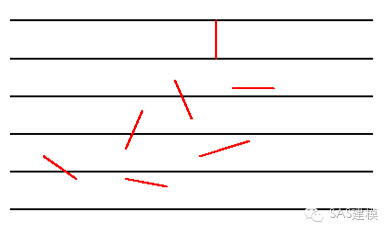
蒙特卡洛方法的最初的应用是1777年法国数学家Buffon提出利用投针试验求解的蒲丰投针问题:设我们有一个以平行且等距木纹铺成的地板(如图),现在随意抛一支长度比木纹之间距离小的针,求针和其中一条木纹相交的概率。
这一方法的步骤是:
1) 取一张白纸,在上面画上许多条间距为a的平行线。
2) 取一根长度为l(l≤a/2) 的针,随机地向画有平行直线的纸上掷n次,观察针与直线相交的次数,记为m。
3)计算针与直线相交的概率.
18世纪,法国数学家布丰和勒可莱尔提出的“投针问题”,记载于布丰1777年出版的著作中:“在平面上画有一组间距为a的平行线,将一根长度为l(l=a/2)的针任意掷在这个平面上,求此针与平行线中任一条相交的概率。”
布丰本人证明了,这个概率是:
![]()
(其中π为圆周率)
由于它与π有关,于是人们想到利用投针试验来估计圆周率的值。
Buffon惊奇地发现:有利的扔出与不利的扔出两者次数的比,是一个包含π的表示式.如果针的长度等于a/2,那么有利扔出的概率为1/π.扔的次数越多,由此能求出越为精确的π的值。
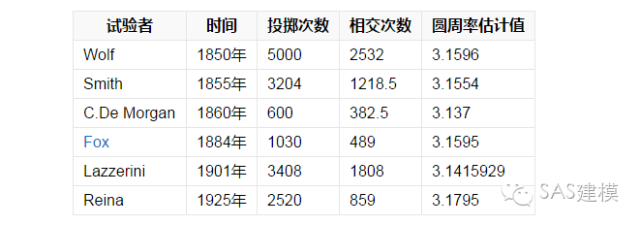
下面是利用这个公式,用概率的方法得到圆周率的近似值的一些资料。
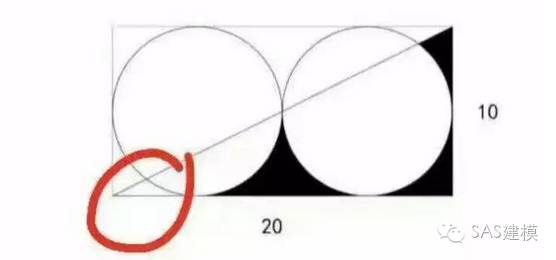
参考这个方法,回到我们的问题,我们可以在图形上随机大量的投点,观察投点在所求区域的概率,从而通过大数定理逼近所求区域的面积。首先我们先简化一下原问题,图中(阴影部分的面积+红色圆圈内的类似三角形的区域面积)*2其实等于长方形面积减去两个圆的面积,因此:
阴影部分的面积
=(200-π*5*5*2)/2-红色圆圈内的类似三角形的区域面积
=100-25*π-红色圆圈内的类似三角形的区域面积
那么我们估计一下红色圆圈内的类似三角形的区域面积就行啦。
面积的估算使用以下macro,其中time为模拟次数。核心思想就是在一个面积可求的区域内随机投点,计算点在所求区域的概率,并通过大数法则逼近所求区域的面积与可求面积区域的面积比,从而计算得到所求区域的面积。
output;
end;
run;
/*对在目标范围内的点进行标记*/
data count;
set random;
if x<5 and y<5 and y<0.5*x and (x-5)*(x-5)+(y-5)*(y-5)>25 then flag=1;
else flag=0;
run;
/*计算面积*/
proc sql;
create table area&time as select
100-25*constant(‘pi’)-sum(flag)/count(flag)*200 as area&time
from count;
quit;
/*打印面积*/
proc print data=area&time;
run;
%mend;
/*随机生成一亿个样本点来估计所求面积*/
%area(100000000);
经过这一亿次模拟,最终得到面积的估计值为19.5036。
方法、程序和结果看似都很圆满。
但是。。。最后的最后,一亿次模拟太费时,电脑破跑的又慢。。。
红包被隔壁寝室的哥们抢先一步夺走了。。。
来自 SAS建模